CF938C

题目

Let’s denote a m-free matrix as a binary (that is, consisting of only 1’s and 0’s) matrix such that every square submatrix of size m × m of this matrix contains at least one zero.

Consider the following problem:

You are given two integers n and m. You have to construct an m-free square matrix of size n × n such that the number of 1’s in this matrix is maximum possible. Print the maximum possible number of 1’s in such matrix.

You don’t have to solve this problem. Instead, you have to construct a few tests for it.

You will be given t numbers x1, x2, …, $x_t$. For every 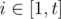, find two integers n and m (n ≥ m) such that the answer for the aforementioned problem is exactly x .

Input

The first line contains one integer t (1 ≤ t ≤ 100) — the number of tests you have to construct.

Then t lines follow, i-th line containing one integer x (0 ≤ x ≤ $10^9$).

Output

For each test you have to construct, output two positive numbers n and m (1 ≤ m≤ n ≤ 10^9) such that the maximum number of 1’s in a m-free n × n matrix is exactly x. If there are multiple solutions, you may output any of them; and if this is impossible to construct a test, output a single integer  - 1.

Example

input

3
21
0
1

output

5 2
1 1
-1

题解

不难发现对于每一个子阵,总是最右下方的那个地方置为0最合适,因为这样的潜力最大.

问题转化为是否存在n,m使得$n^2$-$[n/m]^2$=x.

既是 $a^2-b^2=C $

转化一下 $ (a+b)(a-b)=C$

然后再分解因子搞一搞就可以了.

代码

#include<cstdio>
const int INF=1e9;
int m,n;
bool judge(int t,int s){
	if(((s+t)&1)||((s-t)&1))return false;
	n=(s+t)/2;
	//printf("n=%d\n",n);
	if(n>INF||n<1)return false;
	int tmp=(s-t)/2;
	for(int i=1;i<=n;++i){
		if(n/i<tmp||n/i<1){
			return false;
		}
		if(n/i==tmp){
			m=i;
			return true;
		}
	}
	return false;
}
int main(){
	int T;scanf("%d",&T);
	while(T--){
		int x;scanf("%d",&x);
		if(x==0){
			printf("1 1\n");
			continue;
		}

		bool tag=false;
		for(int i=1;i*i<=x;++i){
			if(x%i==0&&judge(i,x/i)){
				printf("%d %d\n",n,m);
				tag=true;
				break;
			}
		}
		if(!tag)printf("-1\n");
	}
	return 0;
}