CF909E Coprocessor

题目:

You are given a program you want to execute as a set of tasks organized in a dependency graph. The dependency graph is a directed acyclic graph: each task can depend on results of one or several other tasks, and there are no directed circular dependencies between tasks. A task can only be executed if all tasks it depends on have already completed.

Some of the tasks in the graph can only be executed on a coprocessor, and the rest can only be executed on the main processor. In one coprocessor call you can send it a set of tasks which can only be executed on it. For each task of the set, all tasks on which it depends must be either already completed or be included in the set. The main processor starts the program execution and gets the results of tasks executed on the coprocessor automatically.

Find the minimal number of coprocessor calls which are necessary to execute the given program.

Input

The first line contains two space-separated integers N (1 ≤ N ≤ $10^5$) — the total number of tasks given, and M (0 ≤ M ≤ $10^5$) — the total number of dependencies between tasks.

The next line contains N space-separated integers 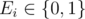img. If $E_i​$= 0, task i can only be executed on the main processor, otherwise it can only be executed on the coprocessor.

The next M lines describe the dependencies between tasks. Each line contains two space-separated integers T1 and T2 and means that task T1 depends on task T2 (T1 ≠ T2). Tasks are indexed from 0 to N - 1. All M pairs (T1, T2) are distinct. It is guaranteed that there are no circular dependencies between tasks.

Output

Output one line containing an integer — the minimal number of coprocessor calls necessary to execute the program.

Examples

input

1
2
3
4
5
4 3
0 1 0 1
0 1
1 2
2 3

output

1
2

input

1
2
3
4
5
4 3
1 1 1 0
0 1
0 2
3 0

output

1
1

思路:

其实思路还是比较好想的,肯定是要从入度为0的点入手.

solution 1

1
2
3
4
5
6
7
8
9
10
我们不难想到这样一个策略,从入度为0的点入手,如果当前处理的是0,那么res+1,否则一直继续.
然后WA3.
那么我们考虑这样一组数据:
5 4
1 1 0 1 0
0 1
0 2
0 3
0 4
显然不正确,原来是没有考虑顺序,我们先拿0,再拿1不就可以了么.

solution 2 

1
2
3
4
5
6
7
8
然后依然WA3.
我们考虑这样一组数据:
5 3
0 1 0 1 0
1 0
2 1
4 3
也不正确

solution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
我们维护两个入读为0的队列分别存值为0的点和值为1的点,我们先把度为0的点的队列拿光后,再把度为1的点的队列中点拿光,这样一直做下去就可以了.
#include<cstdio>
#include<cstring>
#include<vector>
#include<queue>
using namespace std;
const int MAXV=1e5+7,MAXE=1e5+7;
struct edge{
	int to,next;
}es[MAXE];
int head[MAXV],tot;
void init(){
	tot=0;
	memset(head,-1,sizeof(head));
}
void addEdge(int a,int b){
	es[tot].to=b;
	es[tot].next=head[a];
	head[a]=tot++;
}
int num[MAXV],in[MAXV];
int main(){
	int V,E;scanf("%d%d",&V,&E);
	for(int i=0;i<V;++i)scanf("%d",&num[i]);
	init();
	for(int i=0;i<E;++i){
		int a,b;scanf("%d%d",&a,&b);
		addEdge(b,a);
		in[a]++;
	}
	queue<int>q1,q2;
	for(int i=0;i<V;++i){
		if(in[i]==0){
			if(num[i]==0)q1.push(i);
			else q2.push(i);
		}
	}
	int res=0;
	int cnt=V;
	while(cnt){
		while(!q1.empty()){
			int no=q1.front();q1.pop();
			--cnt;
			for(int i=head[no];~i;i=es[i].next){
				int v=es[i].to;
				in[v]--;
				if(in[v]==0){
					if(num[v]==0)q1.push(v);
					else q2.push(v);
				}
			}
		}
		bool flag=false;
		while(!q2.empty()){
			int no=q2.front();q2.pop();
			--cnt;
			flag=true;
			for(int i=head[no];~i;i=es[i].next){
				int v=es[i].to;
				in[v]--;
				if(in[v]==0){
					if(num[v]==0)q1.push(v);
					else q2.push(v);
				}
			}
		}
		if(flag)++res;
	}
	printf("%d\n",res);
	return 0;
}
|